Dlaczego istotność statystyczna jest ważna?
Dowiedz się, dlaczego istotność statystyczna ma znaczenie w analizie danych, badaniach naukowych i podejmowaniu decyzji biznesowych. Poznaj wartości p, testowan...
Dowiedz się, jak istotność statystyczna pozwala określić, czy wyniki są rzeczywiste, czy przypadkowe. Poznaj p-wartości, testowanie hipotez i praktyczne zastosowania dla Twojego biznesu w 2025 roku.
Istotność statystyczna służy do określania, czy wynik jest przypadkowy, czy spowodowany jakimś istotnym czynnikiem. Jeśli wynik jest statystycznie istotny, to prawdopodobieństwo, że wystąpił przypadkowo, jest niewielkie.
Istotność statystyczna to podstawowe pojęcie w analizie danych, które pozwala odróżnić rzeczywiste efekty od przypadkowych wahań w Twoich danych. Prowadząc eksperymenty, ankiety czy analizując wskaźniki biznesowe, potrzebujesz wiarygodnej metody, by określić, czy zaobserwowane wzorce są rzeczywiste, czy tylko wynikiem przypadku. Istotność statystyczna dostarcza tego krytycznego narzędzia, wykorzystując zasady matematyczne do oceny prawdopodobieństwa, że zaobserwowane wyniki pojawiłyby się, gdyby rzeczywiście nie było żadnego efektu lub różnicy między porównywanymi grupami.
Pojęcie to wywodzi się z prac statystyka Ronalda Fishera z początku XX wieku i stało się fundamentem testowania hipotez we wszystkich dziedzinach wykorzystujących analizę danych. Od badań farmaceutycznych potwierdzających skuteczność leków po firmy e-commerce optymalizujące współczynniki konwersji – istotność statystyczna oddziela wartościowe wnioski od mylących konkluzji. Zrozumienie, jak działa istotność statystyczna, daje Ci możliwość podejmowania świadomych decyzji opartych na twardych dowodach, a nie na intuicji czy przypadku.
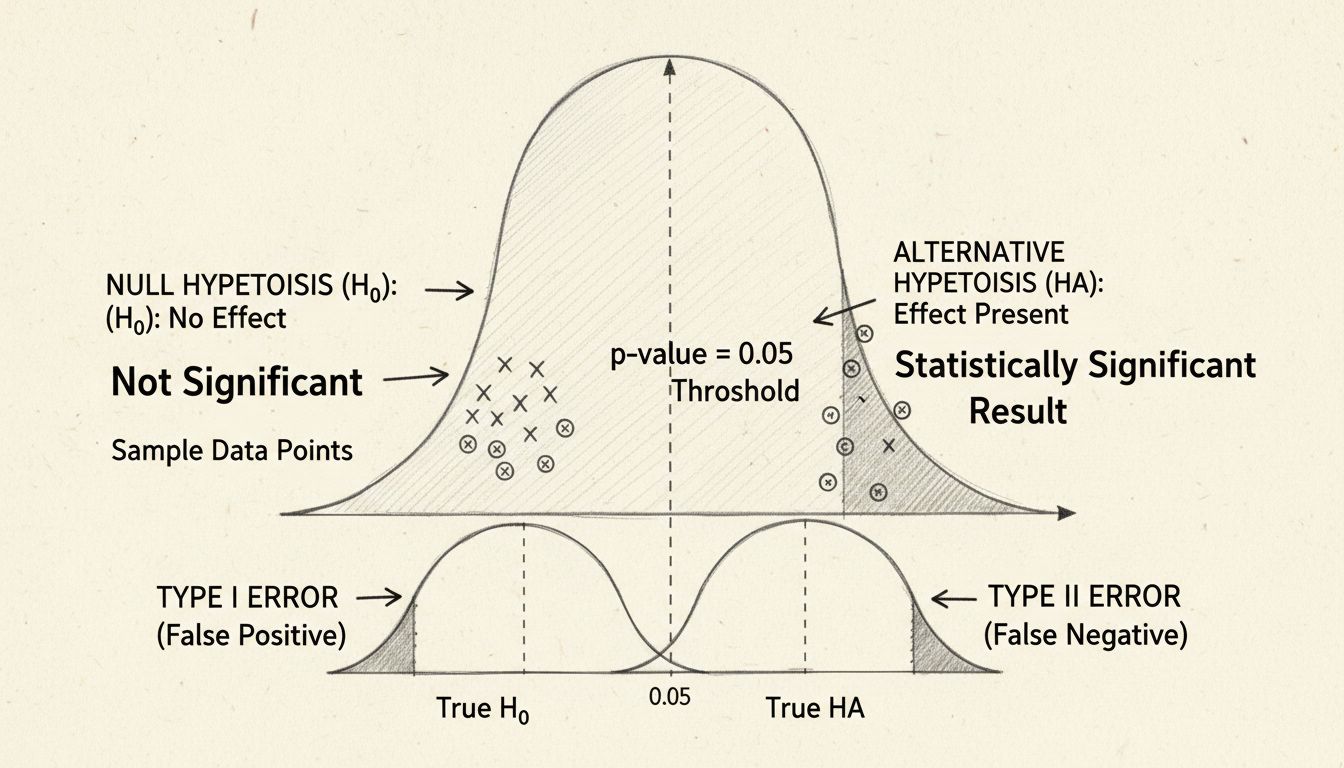
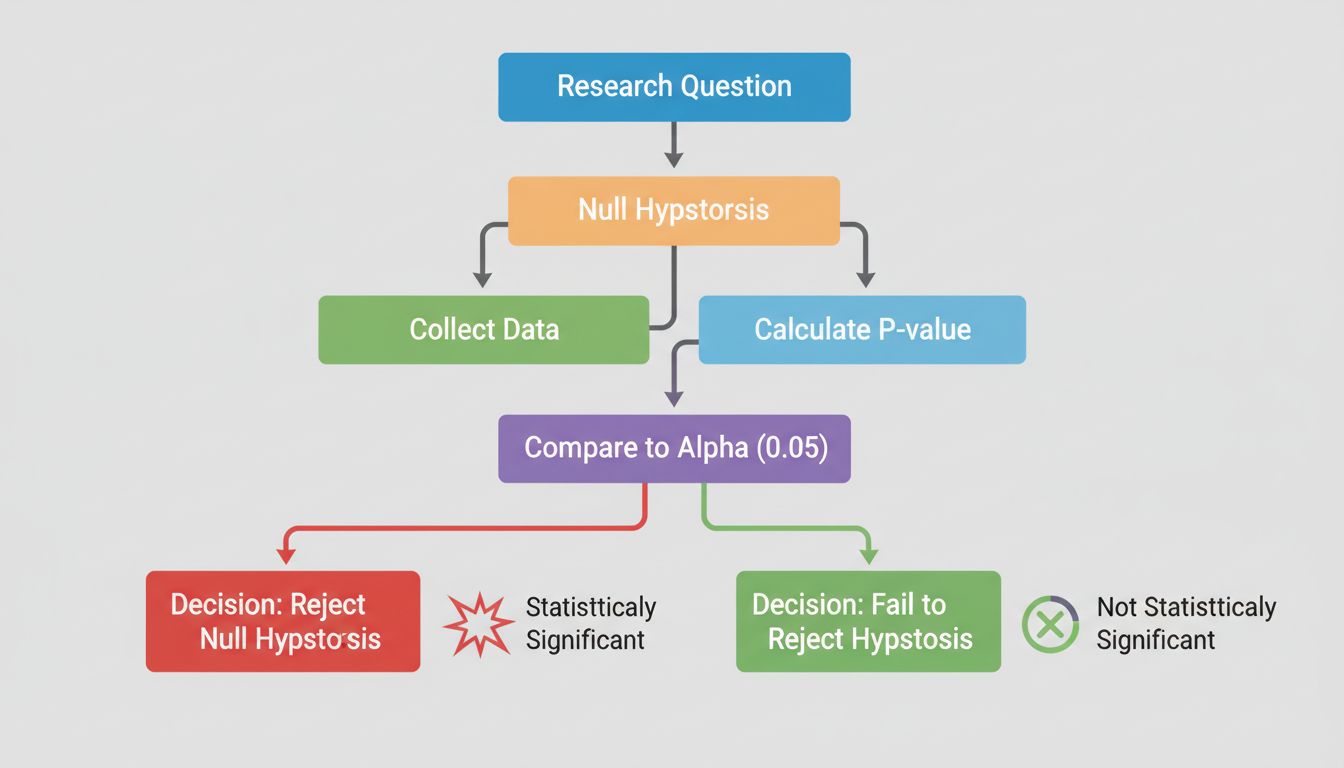
Sednem istotności statystycznej jest testowanie hipotez, czyli uporządkowana metoda oceny twierdzeń na temat danych. Proces rozpoczyna się od sformułowania dwóch konkurencyjnych hipotez: hipotezy zerowej oraz hipotezy alternatywnej. Hipoteza zerowa zakłada brak rzeczywistego efektu lub różnicy między badanymi grupami — reprezentuje ona status quo lub założenie, że każda zaobserwowana różnica to jedynie wynik przypadku. Hipoteza alternatywna natomiast sugeruje istnienie rzeczywistego efektu lub różnicy.
Rozważ praktyczny przykład: testujesz, czy nowa kampania marketingu afiliacyjnego generuje wyższy współczynnik konwersji niż dotychczasowa metoda. Hipoteza zerowa głosi, że oba podejścia dają identyczne współczynniki konwersji, zaś hipoteza alternatywna zakłada, że nowa kampania daje inny wynik. Test statystyczny ocenia, którą z hipotez silniej wspierają dane. Takie podejście zabezpiecza przed subiektywnym wybieraniem wyników potwierdzających własne oczekiwania — wymaga bowiem udowodnienia, że odkrycie jest mało prawdopodobne jako efekt przypadku.
Piękno testowania hipotez tkwi w jego obiektywizmie. Zamiast polegać na subiektywnych ocenach, używasz matematycznych obliczeń, by sprawdzić, czy dane dostarczają wystarczających dowodów do odrzucenia hipotezy zerowej. Jeśli dowody są wystarczająco silne, możesz z przekonaniem stwierdzić, że zaobserwowany efekt jest statystycznie istotny — czyli mało prawdopodobny, by był dziełem przypadku.
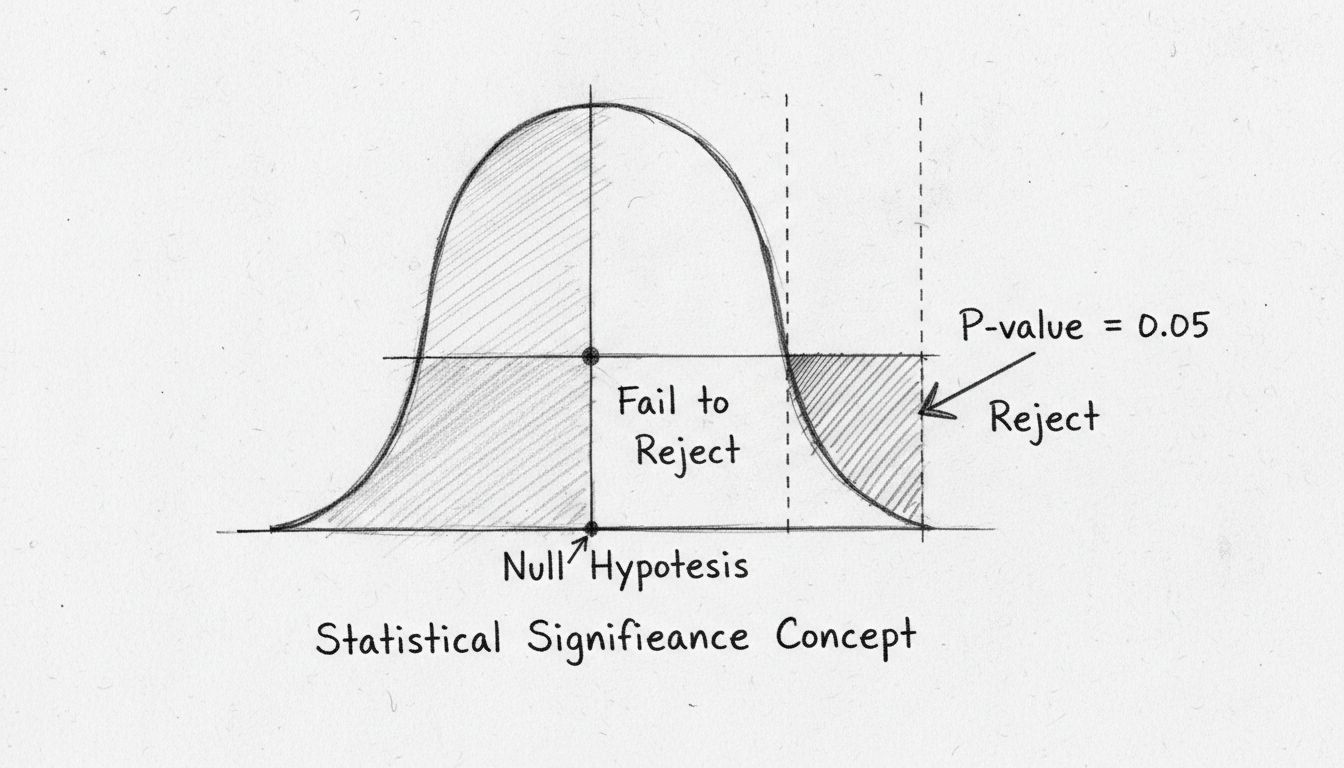
P-wartość to prawdopodobnie najczęściej stosowana miara w testach istotności statystycznej, choć bywa często źle rozumiana. P-wartość oznacza prawdopodobieństwo uzyskania zaobserwowanego wyniku (lub bardziej skrajnego), gdyby hipoteza zerowa była prawdziwa. Innymi słowy, odpowiada na pytanie: „Jak bardzo prawdopodobne jest, że zobaczę takie dane, jeśli w rzeczywistości nie ma efektu?” Niska p-wartość wskazuje, że zaobserwowane wyniki byłyby bardzo mało prawdopodobne przy prawdziwości hipotezy zerowej, sugerując, że hipoteza zerowa jest prawdopodobnie fałszywa, a efekt jest rzeczywisty.
Konwencjonalny próg istotności statystycznej to p-wartość równa 0,05 lub mniej, co oznacza 5% prawdopodobieństwo, że wynik jest dziełem przypadku. Akceptujesz tym samym 5% ryzyko błędnego odrzucenia hipotezy zerowej, gdy jest ona prawdziwa (tzw. błąd pierwszego rodzaju). Jednak ten próg jest dość arbitralny i zależny od dziedziny oraz kontekstu. W badaniach medycznych, gdzie konsekwencje fałszywych pozytywów są poważne, często stosuje się bardziej rygorystyczny próg 0,01 (1%). Natomiast w badaniach eksploracyjnych lub na wczesnym etapie dopuszczalny bywa próg 0,10 (10%).
| Zakres p-wartości | Interpretacja | Typowa decyzja |
|---|---|---|
| p < 0,01 | Wysoce istotny | Silny dowód przeciw hipotezie zerowej |
| 0,01 ≤ p < 0,05 | Istotny | Umiarkowany dowód przeciw hipotezie zerowej |
| 0,05 ≤ p < 0,10 | Granicznie istotny | Słaby dowód przeciw hipotezie zerowej |
| p ≥ 0,10 | Nieistotny | Brak wystarczających dowodów do odrzucenia hipotezy zerowej |
Ważne jest zrozumienie, czego p-wartość nie oznacza. P-wartość 0,03 nie oznacza, że istnieje 97% prawdopodobieństwo prawdziwości hipotezy. Nie mierzy też wielkości czy praktycznego znaczenia efektu. Wynik statystycznie istotny może oznaczać efekt na tyle mały, że nie ma on znaczenia w praktyce. Rozróżnienie między istotnością statystyczną a praktyczną to jeden z najczęstszych błędów w analizie danych.
Podczas gdy p-wartości informują, czy efekt istnieje, przedziały ufności dostarczają kluczowych informacji o jego wielkości i precyzji. Przedział ufności to zakres wartości, który najprawdopodobniej zawiera rzeczywistą wielkość efektu, obliczony z określonym poziomem ufności (zwykle 95%). Jeśli testujesz, czy nowa funkcja programu partnerskiego zwiększa prowizje, 95% przedział ufności może wskazywać, że rzeczywisty wzrost mieści się w granicach od 2% do 8%, z 95% pewnością, że prawdziwa wartość znajduje się w tym przedziale.
Przedziały ufności mają kilka przewag nad samymi p-wartościami. Po pierwsze, przekazują zarówno kierunek, jak i wielkość efektu, dając pełniejszy obraz wyników. Po drugie, pomagają ocenić znaczenie praktyczne — nawet jeśli efekt jest istotny statystycznie, ale przedział ufności wskazuje, że jest znikomy, wdrożenie może się nie opłacać. Po trzecie, wąskie przedziały ufności oznaczają precyzyjne oszacowania, a szerokie — większą niepewność.
Wielkość efektu mierzy siłę związku między zmiennymi lub wielkość różnicy między grupami. Popularne miary wielkości efektu to d Cohena (dla porównania średnich), współczynniki korelacji czy ilorazy szans. Efekt może być statystycznie istotny, a jednocześnie mieć niewielką wielkość, co oznacza znikomy wpływ praktyczny. Z drugiej strony, duża wielkość efektu może nie osiągnąć istotności przy zbyt małej próbie. Profesjonalni analitycy zawsze raportują wielkość efektu razem z p-wartością, by dać pełny obraz wyników.
Wielkość próby odgrywa kluczową rolę w określaniu istotności statystycznej. Większe próby dają więcej informacji o populacji i zmniejszają wpływ przypadkowych wahań, co ułatwia wykrycie rzeczywistych efektów. Z kolei małe próby są bardziej podatne na przypadkowe fluktuacje, mogąc prowadzić zarówno do fałszywych pozytywów (wykrycie nieistniejącego efektu), jak i fałszywych negatywów (przeoczenie rzeczywistego efektu).
Związek między wielkością próby a mocą statystyczną jest podstawą projektowania badań. Moc statystyczna to prawdopodobieństwo prawidłowego odrzucenia hipotezy zerowej, gdy jest ona fałszywa — czyli zdolność wykrycia rzeczywistego efektu. Większość badaczy dąży do mocy na poziomie 0,80 (80%), akceptując 20% szansy przeoczenia prawdziwego efektu. Osiągnięcie tego poziomu wymaga odpowiednio dużej próby, zależnej od oczekiwanej wielkości efektu, wybranego poziomu istotności oraz rodzaju testu statystycznego.
Przed rozpoczęciem badania lub eksperymentu należy wykonać analizę mocy, by określić wymaganą wielkość próby. Pozwoli to uniknąć marnowania zasobów na zbyt małe badania (które nie wykryją efektu), jak i zbyt duże, pochłaniające niepotrzebnie czas i pieniądze. W kontekście marketingu afiliacyjnego oznacza to określenie, ile konwersji lub kliknięć musisz zaobserwować, by móc z przekonaniem stwierdzić, że zmiana kampanii miała realny wpływ.
Różne pytania badawcze i typy danych wymagają różnych testów statystycznych. Wybór testu zależy od liczby porównywanych grup, rozkładu danych, niezależności próbek oraz typu zmiennej wynikowej (ciągła, kategoryczna itp.).
Test t-Studenta porównuje średnie dwóch grup i jest jednym z najczęściej stosowanych testów. Nadaje się do danych ciągłych (np. kwoty przychodów) i pozwala sprawdzić, czy dwie grupy różnią się istotnie. Test uwzględnia zmienność wewnątrz grup i wielkości prób, generując statystykę t porównywaną z wartością krytyczną.
Test chi-kwadrat stosuje się do danych kategorycznych, by sprawdzić, czy obserwowane częstości różnią się istotnie od oczekiwanych. Jeśli analizujesz, czy kanał afiliacyjny (e-mail, social media, reklamy display) wpływa na współczynnik konwersji, właściwy będzie test chi-kwadrat.
ANOVA (analiza wariancji) rozszerza test t na porównanie średnich w trzech lub więcej grupach jednocześnie, zapobiegając problemowi wielokrotnego testowania, który zwiększa ryzyko fałszywych pozytywów.
Test U Manna-Whitneya i test rang Wilcoxona to nieparametryczne alternatywy stosowane, gdy dane nie spełniają założeń testów parametrycznych, np. gdy rozkład nie jest normalny.
W biznesie istotność statystyczna kieruje kluczowymi decyzjami w wielu obszarach. Zespoły marketingowe stosują testy A/B z istotnością statystyczną, by sprawdzić, czy zmiany na stronie, tematy e-maili lub kreacje reklam rzeczywiście poprawiają wskaźniki efektywności. Zamiast polegać na intuicji lub obserwacjach z małych próbek, firmy oparte na danych ustalają progi istotności przed uruchomieniem testów, gwarantując podejmowanie decyzji na podstawie wiarygodnych dowodów.
W marketingu afiliacyjnym istotność statystyczna pomaga wskazać, którzy afilianci, kampanie i strategie promocyjne faktycznie generują przychód, a które wydają się skuteczne tylko przez przypadkowe wahania. Analizując, czy nowa struktura prowizji zwiększa skuteczność afiliantów, testy statystyczne chronią przed kosztownymi zmianami opartymi na krótkoterminowych fluktuacjach. Zaawansowana platforma analityczna PostAffiliatePro umożliwia śledzenie wskaźników afiliacyjnych z rygorem statystycznym, co pozwala na pewną optymalizację decyzji.
W badaniach farmaceutycznych i medycznych istotność statystyczna decyduje, czy nowe terapie są wystarczająco skuteczne, by uzyskać zgodę na stosowanie. Badania kliniczne muszą wykazać, że korzyści leku są istotne statystycznie, zanim będzie on przepisany pacjentom. Stawka jest wysoka, dlatego badania medyczne zazwyczaj stosują bardziej rygorystyczne progi istotności niż inne dziedziny.
Jednym z najczęstszych nieporozumień jest przekonanie, że istotność statystyczna dowodzi przyczynowości. Statystycznie istotna korelacja między dwiema zmiennymi nie oznacza, że jedna powoduje drugą. Klasycznym przykładem jest silna korelacja między premierami filmów Nicolasa Cage’a a utonięciami w basenach — oczywiście jedno nie powoduje drugiego. Istotność statystyczna jedynie wskazuje, że związek jest mało prawdopodobny jako dzieło przypadku; dowód przyczynowości wymaga dodatkowych przesłanek, takich jak logiczny mechanizm, kolejność czasowa i kontrolowane eksperymenty.
Kolejnym błędem jest p-hacking lub przekopywanie danych, czyli wykonywanie wielu testów statystycznych na tym samym zbiorze, aż pojawią się istotne wyniki. Takie podejście sztucznie zwiększa szansę na fałszywe pozytywy, ponieważ przy odpowiednio wielu testach zawsze coś wyjdzie istotnego przypadkowo. Jeśli wykonasz 20 niezależnych testów przy progu 0,05, statystycznie jeden wynik okaże się istotny wyłącznie przez przypadek. Odpowiedzialni badacze z góry określają hipotezy oraz testy statystyczne, zapobiegając temu problemowi.
Złą interpretacją jest również traktowanie wyników nieistotnych jako dowód braku efektu. Wynik nieistotny nie oznacza, że efekt nie istnieje; oznacza jedynie brak wystarczających dowodów do odrzucenia hipotezy zerowej. Może to wynikać z niewystarczającej próby, dużej zmienności danych lub faktycznego braku efektu. Brak dowodu to nie dowód braku.
Dziedzina statystyki stale się rozwija, a coraz częściej podkreśla się ograniczenia tradycyjnych podejść opartych wyłącznie na p-wartościach. Wielu statystyków postuluje bardziej zniuansowaną analizę, łączącą p-wartości z wielkością efektu, przedziałami ufności i metodami bayesowskimi. Statystyka bayesowska, która uwzględnia wcześniejszą wiedzę i aktualizuje przekonania na podstawie nowych danych, stanowi alternatywę, którą niektórzy badacze uznają za bardziej intuicyjną i elastyczną niż podejścia klasyczne.
Coraz większą popularność zdobywają testy sekwencyjne i projekty adaptacyjne, pozwalające monitorować wyniki w miarę pojawiania się danych i podejmować decyzje o kontynuacji, modyfikacji lub zakończeniu badania na podstawie analiz pośrednich. To szczególnie przydatne w biznesie, gdzie decyzje trzeba podejmować szybko. Narzędzia takie jak Stats Engine firmy Statsig wdrażają testy sekwencyjne z kontrolą współczynnika fałszywych odkryć, umożliwiając szybsze i bardziej precyzyjne podejmowanie decyzji podczas eksperymentów.
Kryzys replikacyjny w nauce dodatkowo podkreślił znaczenie właściwego rozumienia istotności statystycznej. Wiele opublikowanych badań nie daje się powtórzyć, częściowo dlatego, że naukowcy i czasopisma koncentrowały się zbyt mocno na osiągnięciu istotności statystycznej, ignorując wielkość efektu i znaczenie praktyczne. W najbliższych latach nacisk przesuwa się ku transparentności, prerejestracji badań i raportowaniu wszystkich wyników — niezależnie od istotności.
Aby skutecznie korzystać z istotności statystycznej, ustal poziom istotności i wymaganą wielkość próby przed rozpoczęciem analizy. Chroni to przed pokusą dostosowywania progów po zobaczeniu wyników. Zawsze raportuj wielkość efektu i przedziały ufności obok p-wartości, by dać pełny obraz wyników. Oceń znaczenie praktyczne: wynik istotny statystycznie może być zbyt mały, by miał znaczenie w praktyce.
Bądź transparentny w opisie metodyki, w tym w sposobie traktowania braków danych, wartości odstających i wielu porównań. Jeśli przeprowadziłeś wiele testów, zastosuj odpowiednie korekty, jak korekta Bonferroniego, by zachować ogólny poziom istotności. Udokumentuj proces analizy i bądź gotów udostępnić dane oraz kod do weryfikacji i replikacji.
Na koniec pamiętaj, że istotność statystyczna to narzędzie, a nie cel sam w sobie. Pomaga podejmować lepsze decyzje przez ograniczenie wpływu przypadku, ale powinna być łączona z wiedzą ekspercką, praktycznymi uwarunkowaniami i zdrowym rozsądkiem. W marketingu afiliacyjnym istotność statystyczna pomaga wskazać, które strategie faktycznie poprawiają wyniki, ale przy podejmowaniu decyzji strategicznych należy brać pod uwagę także koszty wdrożenia, satysfakcję afiliantów i długoterminową trwałość rozwiązań.
Zaawansowane narzędzia analityczne i raportowe PostAffiliatePro pomagają śledzić wyniki afiliantów z rygorem statystycznym. Dowiedz się, które kampanie rzeczywiście przynoszą rezultaty i optymalizuj program partnerski na podstawie wiarygodnych danych.

Dowiedz się, dlaczego istotność statystyczna ma znaczenie w analizie danych, badaniach naukowych i podejmowaniu decyzji biznesowych. Poznaj wartości p, testowan...
Istotność statystyczna wyraża wiarygodność zmierzonych danych, pomagając firmom odróżnić rzeczywiste efekty od przypadku i podejmować świadome decyzje, szczegól...

Opanuj istotność statystyczną w testach A/B dla kampanii afiliacyjnych w branży bukmacherskiej.
Zgoda na Pliki Cookie
Używamy plików cookie, aby poprawić jakość przeglądania i analizować nasz ruch. See our privacy policy.